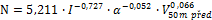Stanovení vlivu geometrie okružní křižovatky na rychlost průjezdu a bezpečnost
Nová výstavba nebo přestavba stávající křižovatky na okružní je běžnou praxí rozvoje a údržby silniční infrastruktury. Tento článek je zaměřen na analýzu přímého průjezdu vozidla okružní křižovatkou. Měření probíhalo pomocí GPS jednotky umístěné v měřícím vozidle. Realizovali jsme cca 150 přímých průjezdů na 11 okružních křižovatkách v městě Brně. Identifikovali jsme parametry směrového polygonu jízdy vozidla: přímkovou a obloukovou část průjezdu a hodnoty úhlu na vjezdu, úhlu na přímém průjezdu, úhlu na výjezdu, poloměru vjezdu, průjezdu a výjezdu. Hlavním přínosem práce je stanovení vlivu geometrie okružní křižovatky na rychlost průjezdu a bezpečnost. Závěry potvrzují nutnost dodržování vhodných návrhových parametrů křižovatky, abychom zaručili její bezpečnost a propustnost.
Úvod
Okružní křižovatky (OK) představují jeden z nejdynamičtěji rozšiřujících se typů křižovatek na silniční infrastruktuře v ČR. Tento typ křižovatky se realizuje jako novostavba, ale častěji jako přestavba stávající stykové nebo průsečné křižovatky. Ke stavbě OK se přistupuje především z pohledu propustnosti a čím dál častěji i z pohledu bezpečnosti. Bezpečnost vychází z geometrického uspořádání křižovatky, které má přímý vliv na trajektorii projíždějících vozidel. Vybudováním OK dochází ke vzniku bariéry v přímém směru jízdy, tj. středového ostrova. Což řidiče motivuje upravit rychlost vozidla. Na území ČR jsme identifikovali cca 1200 OK.
Současný stav poznání
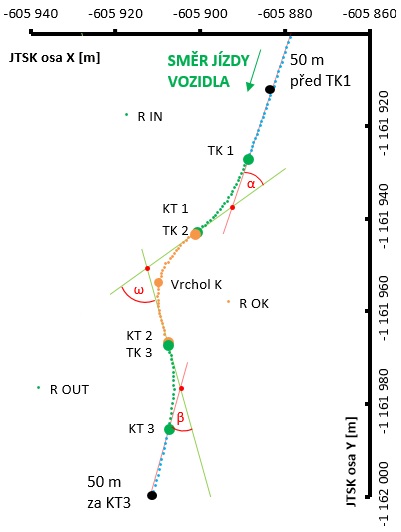
Přímý průjezd vozidla OK je v této práci definován mezi dvěma protilehlými rameny OK. Trajektorie představuje pohyb vozidla (zelené body na obr. 01). Tato práce uvažuje, že trajektorii vozidla na průjezdu křižovatkou lze rozložit a zjednodušit pomocí prvků směrového polygonu (přímky) a oblouků. Trajektorie obsahuje přímku na vjezdu, pravý směrový oblouk na vjezdu, levý směrový oblouk na okruhu křižovatky, pravý směrový oblouk na výjezdu křižovatky a přímku za výjezdem. Mezi přilehlými oblouky uvažujeme inflexní bod (na obr. 01 bod TK=KT). Naměřenou krátkou (L<1m) mezipřímou zanedbáváme. Tečny tvoří směrový polygon. Přímky polygonu spolu svírají úhly (postupně α, ω, β).
|
|
|
obr. 01.Parametry směrového polygonu přímého průjezdu vozidla OK |
Úhel na vjezdu OK α (viz obr. 01) představuje změnu směru jízdy vozidla při vjezdu na okružní pás. Úhel na přímém průjezdu křižovatkou ω (viz obr. 01) představuje změnu směru pohybu vozidla při objíždění středového ostrova. Úhel na výjezdu OK β (viz obr. 01) představuje změnu směru jízdy vozidla při výjezdu z okružního pásu.
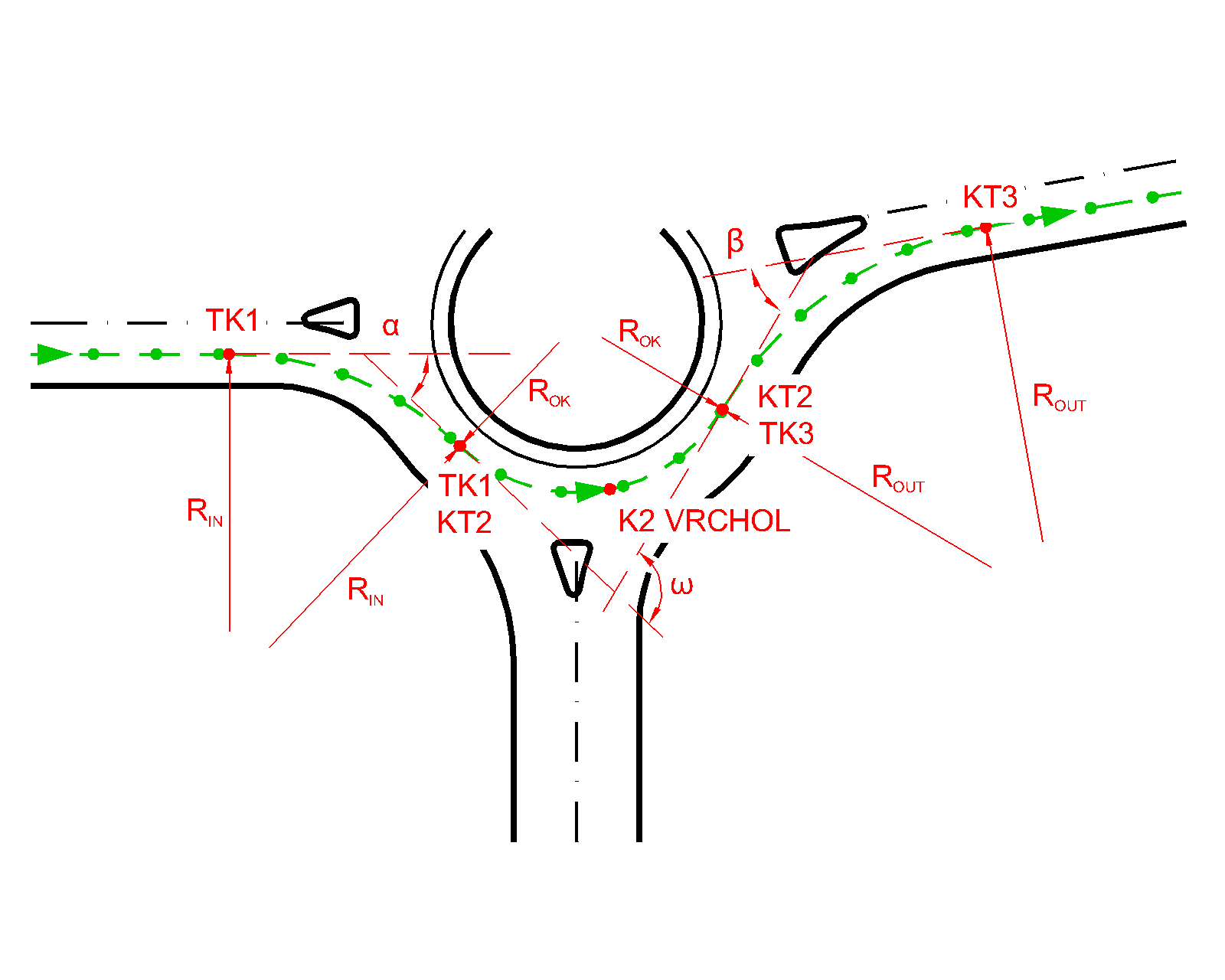
U špatně navržených OK nabývají úhly α, ω nebo β hodnot blížících se nule. Vozidlo pak projíždí téměř nebo úplně po přímce (viz obr. 03). Následkem toho nedochází k redukci rychlosti. Na obr. 02 je zobrazen vliv zmenšujícího se poloměru středního ostrova na hodnotu úhlu na přímém průjezdu ω.
|
|
|
|
|
obr. 02.Úhel na přímém průjezdu ω |
obr. 03.Nevhodně navržená OK – možný přímý průjezd |
obr. 04.Vhodně navržená křižovatka |
OK s vyššími hodnotami úhlu na přímém průjezdu ω (viz obr. 04) vyvolávají snížení rychlosti vozidla, tím dojde k úpravě odstupů vozidel a jejich vyšší využitelnosti při zařazování vozidel z jiných směrů. Dojde tak ke zvýšení propustnosti křižovatky a zároveň ke zvýšení bezpečnosti vlivem nízkých rychlostí. Rychlost vozidla na průjezdu obloukem by se měla pohybovat maximálně mezi 30 – 35 km/h (dle TP 135 [02]), jinak dochází ke zvýšení počtu DN nebo závažnějším následkům. Do směrového polygonu jsou vloženy směrové oblouky, které nahrazují reálnou volantovou křivku. Oblouk náleží vždy mezi dvě tečny (přímky), které svírají příslušný směrový úhel (α, ω, β). Návrhovými poloměry na vjezdu/průjezdu/výjezdu OK se zabývá např. publikace Traffic and Highway Engineering [09], která je odvozuje dle obalových křížovek jednotlivých typů vozidel s ohledem na jejich rychlost. V ČSN 73 6102 [01] je uvedena maximální hodnota poloměru R<100 m na přímém průjezdu OK. Nově revidované TP 135 [02] doporučují korigovat průjezd vozidla pomocí pojížděného prstence (podrobněji viz diskuze).
Data
Výběrový soubor pro řešení této úlohy zahrnoval 155 průjezdů měřícího vozidla na 11 OK ve městě Brně (v intravilánu). Jedno měření představovalo přímý průjezd vozidla křižovatkou z vjezdu do protilehlého výjezdu. Průjezdy byly realizovány v běžný pracovní den měsíce října 2016. Cílem bylo získat měření z průjezdů, které byly realizovány bez ovlivnění jinou dopravou. Původní vzorek pro analýzu musel tedy být z důvodu ovlivnění redukován na 92 průjezdů.
tab. 1.Analyzované křižovatky: Brno
|
Okružní křižovatka |
Počet ramen |
Trajektorie Měřené / Validované |
Průměrná hodnota [m] |
Průměr OK |
Průměrná hodnota [ ̊ ] |
|||||
|---|---|---|---|---|---|---|---|---|---|---|
|
α |
ω |
β |
||||||||
| Rin | Rok | Rout | ||||||||
|
Dlouhá x Hraničky |
4 |
21 / 21 |
28,9 |
17,2 |
36,1 |
30 |
37 |
76 |
33 |
|
|
Hlavní x Absolonova |
4 |
10 / 10 |
34,2 |
18,7 |
37,5 |
33 |
35 |
79 |
33 |
|
|
Hudcova x Kytnerova |
3 |
10 / 6 |
27,8 |
15,4 |
33,0 |
30 |
35 |
117 |
39 |
|
|
Hviezdoslavova x Bedřichovická |
4 |
18 / 9 |
55,6 |
24,4 |
52,1 |
27 |
15 |
46 |
16 |
|
|
Jihlavská x Stará dálnice |
4 |
18 / 12 |
37,3 |
19,1 |
34,1 |
35 |
26 |
70 |
32 |
|
|
Koperníkova x Lazaretní |
4 |
10 / 9 |
28,3 |
22,8 |
37,9 |
31 |
36 |
71 |
33 |
|
|
Kšírova x Sokolova |
4 |
21 / 1 |
40,8 |
19,3 |
32,3 |
31 |
31 |
78 |
34 |
|
|
Odbojářská x Nad Kašnou |
4 |
8 / 1 |
> R* |
19,8 |
34,7 |
29 |
2 |
68 |
21 |
|
|
Palachovo náměstí |
4 |
10 / 8 |
27,0 |
23,9 |
25,6 |
48 |
49 |
92 |
50 |
|
|
Slezákova x Kohoutova |
3 |
12 / 6 |
24,0 |
19,1 |
63,7 |
32 |
64 |
75 |
15 |
|
|
Vídeňská x FUTURUM |
4 |
9 / 9 |
33,2 |
20,1 |
26,4 |
35 |
35 |
76 |
40 |
|
Poznámka: * Jedná se o vysokou hodnotu poloměru R, který se blížil téměř přímce.
Měření probíhalo pomocí měřícího vozidla, které obsahuje zařízení pro měření fyzikálních veličin s přesnou lokalizací objektů v systému GPS (jednotka Mti 100-series, horizontální přesnost: 1 m) a videozáznam projížděné komunikace.
Metoda
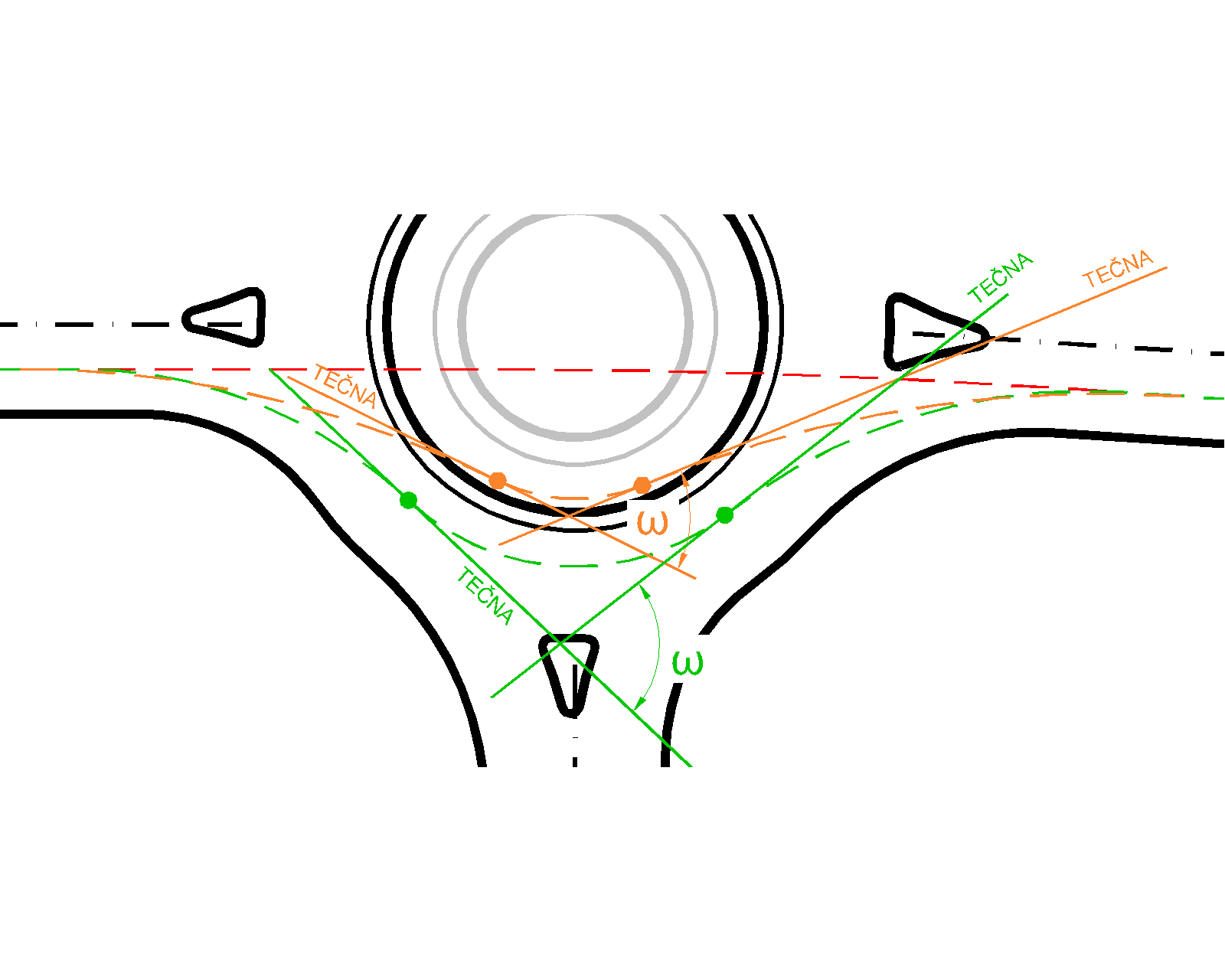
Analýza trajektorie pohybu vozidla spočívá v rozboru skupiny po sobě jdoucích bodů, které definují polohu vozidla vůči počátku souřadnicového systému (původní GPS transformováno do S-JTSK). Trajektorie je vytvořena odečítáním charakteristik polohy měřícího vozidla za pohybu v reálném čase. Skutečná dráha vozidla byla nahrazena řadou bodů, které v pravidelných časových intervalech odečítala jednotka GPS. Pro rozbor je nejpodstatnější směrový úhel φ a odchylka směru Δφ po sobě jdoucích bodů trajektorie. Postup výpočtu následuje.
|
Směrový úhel φi představuje hodnotu ve stupních, kterou nabývá úhel, který svírá kladná osa X a osa směru pohybu k následujícímu bodu (B) ve směru pohybu vozidla. Úhel je stanoven z rozdílu souřadnic po sobě jdoucích bodů (B – A) goniometrickými funkcemi. Odchylka směru Δφi se vypočte ze směrového úhlu φi. Odchylka představuje rozdíl po sobě jdoucích směrových úhlu . Přímý směr pohybu vozidla je prezentován přímkou. Směrový úhel φi pohybujícího se vozidla nabývá stále stejných hodnot (např. směrem na sever = 90°). To znamená, že odchylka směrů Δφi v modelovaném případě nabývá 0. Z důvodu nepřesnosti GPS jednotky se připustila tolerance ± 0,5°. Změna směru pohybu vozidla je prezentována směrovým obloukem. V případě změny směru pohybu vozidla směrový úhel φi nabývá v každém bodě jiné hodnoty až do doby, kdy vozidlo dosáhne svého nového cílového směru (opustí pohyb po oblouku a přejde v přímku). Odchylka směru Δφi v tomto případě nabývá konstantních hodnot (hodnota směrového úhlu se s každým dalším bodem trajektorie mění). |
|
|
obr. 05.Základní konstrukce trajektorie pohybu vozidla pro analýzu jeho pohybu |
Identifikace prvků trajektorie je důležitá kvůli stanovení rychlosti vozidla v jednotlivých prvcích jízdní dráhy a vlivu jejich parametrů.
|
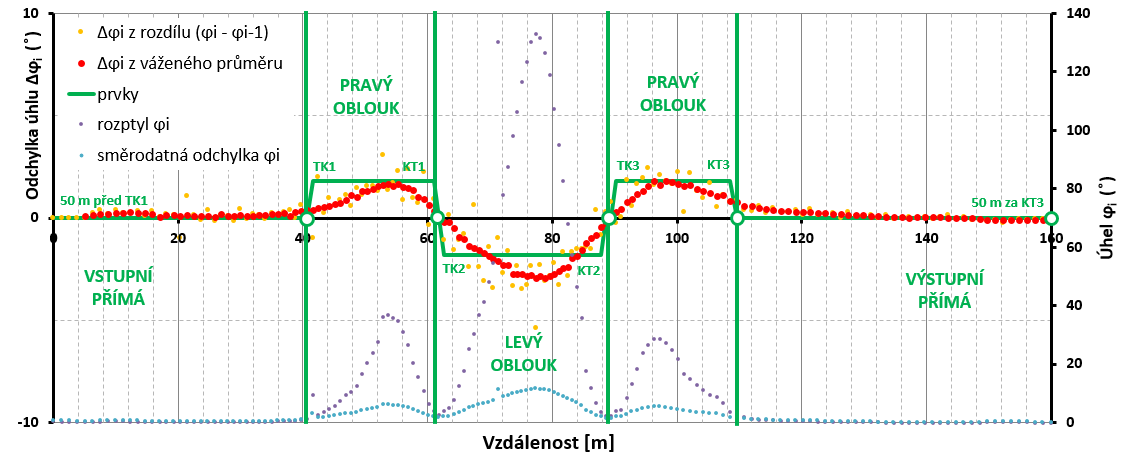
Pro redukci nepřesnosti jednotky GPS bylo provedeno vyrovnání směrových úhlů φi pomocí váženého průměru. Váhu představovala vzdálenost mezi jednotlivými body trajektorie. Průměr se počítal vždy z tolika úseků, jejichž součet délek (vzdáleností) byl < 10 m. Identifikace prvků trajektorie vychází z průběhu vyrovnaného směrového úhlu φi a odchylky směru Δφi (viz obr. 07). Identifikace prvku trajektorie se provádí od prvního směrového úhlu φi kde i=1 až po poslední prvek i=n. Přímka vykazuje jen minimální rozdíl mezi rozptylem a směrodatnou odchylkou směrového úhlu φi (s tolerancí ± 0,5°). Jejich nulové hodnoty představují přímku a hranici obloukových prvků. Pravý oblouk vykazuje kladné hodnoty odchylky směru Δφi. Levý oblouk vykazuje záporné hodnoty odchylky směru Δφi. V první řadě je ale nutné nejprve vyloučit výskyt přímky. Na obr. 06 je znázorněn průběh prvků směrového polygonu trajektorie při průjezdu křižovatkou v tomto pořadí: vjezdová přímka (modré body), pravý oblouk (zelené body), levý oblouk (oranžové body), pravý oblouk (zelené body) a výjezdová přímka (modré body). |
|
|
obr. 06.Konstrukce trajektorie přímého průjezdu na OK (skutečný průjezd) |
U oblouku je nezbytné identifikovat počáteční (TK), mezilehlý blízký prostřednímu (vrchol K) a koncový bod (KT). Řešením soustavy tří rovnic o třech neznámých (dosazením do obecné rovnice pro kružnici se středem v bodě) získáme polohu středu a hodnotu poloměru. Na základě polohy středu kružnice, počátku a konce oblouku se vypočte úhel na vjezdu α, který je dle konstrukce směrového polygonu (přímka, kružnice, přímka) stejný jak v jeho vrcholu, tak ve výseči oblouku. Stejným postupem se stanoví parametry pro všechny oblouky trajektorie vozidla. Na následujícím obr. 07 je prezentována identifikace prvků směrového polygonu trajektorie vozidla na přímém průjezdu OK. Směrové oblouky jsou identifikované na základě nenulových hodnot rozptylu a směrodatné odchylky směrového úhlu Δφi.
|
|
|
obr. 07.Identifikace prvků trajektorie pomocí směrových úhlů φi a jejich odchylek Δφi |
Následuje popis charakteristik průměrného směrového polygonu trajektorie na přímém průjezdu OK z reálného měření pomocí měřícího vozidla. Tyto charakteristiky byly odvozeny pomocí analýzy trajektorie vozidla.
tab. 2.Charakteristiky směrových polygonů výběrového vzorku
|
Charakteristika |
Min. |
Max. |
Průměr |
Směr. odch. |
Jednotka |
|---|---|---|---|---|---|
|
Úhel na vjezdu - Alfa |
0 |
82,69 |
32,39 |
18,489 |
[ ̊ ] |
|
Úhel na výjezdu - Beta |
0 |
236,93 |
67,53 |
36,429 |
[ ̊ ] |
|
Úhel na přímém průjezdu křižovatkou - Omega |
0 |
89,27 |
31,21 |
17,166 |
[ ̊ ] |
|
Poloměr na vjezdu RIN |
- |
134,99 |
35,99 |
18,825 |
[m] |
|
Poloměr na průjezdu ROK |
- |
67,50 |
21,16 |
10,219 |
[m] |
|
Poloměr na výjezdu ROUT |
- |
194,50 |
35,76 |
23,982 |
[m] |
|
Rychlost v bodě 50 m před vjezdem (před TK 1) |
27 |
60 |
41,51 |
7,698 |
[km/h] |
|
Rychlost v bodě TK 1 |
16 |
40 |
30,99 |
5,587 |
[km/h] |
|
Rychlost v bodě KT 1 = KT 2 (KK) |
13 |
36 |
26,26 |
4,631 |
[km/h] |
|
Rychlost v bodě vrchol K2 |
11 |
34 |
23,86 |
4,687 |
[km/h] |
|
Rychlost v bodě KT 2 = KT 3 (KK) |
14 |
50 |
30,59 |
5,688 |
[km/h] |
|
Rychlost v bodě KT 3 |
23 |
52 |
37,63 |
6,691 |
[km/h] |
|
Rychlost v bodě 50 m za výjezdem (za KT 3) |
28 |
68 |
44,03 |
9,328 |
[km/h] |
Výsledky
Pro posouzení vlivu poloměru (RIN, ROK, ROUT) a úhlu (α, ω, β) na rychlost V byl použit Spearmanův korelační koeficient. Korelace vyšší jak 0,5 byla zaznamenána pouze u následujících parametrů:
- rychlost V50m před vjezdem a úhel na vjezdu α,
- rychlost V50m před vjezdem a poloměr vjezdu RIN,
- rychlost VK2vrchol a poloměr průjezdu na okruhu ROK.
Z korelace vyplývá, že vozidlo:
- je 50 m před vjezdem nejvíce ovlivněno poloměrem vjezdu RIN, v následujících bodech průjezdu vliv poloměru vjezdu RIN klesá, vliv poloměru je vyšší než vliv úhlu na vjezdu α,
- v místě napojení na okruh křižovatky (KT1 = TK2) má největší vliv jeho vjezdová rychlost V,
- v místě vrcholu ROK má největší vliv poloměr okruhu ROK, vliv vjezdové rychlosti V je v tomto místě podobný jako vliv úhlu na přímém průjezdu ω,
- v místě vrcholu ROK je obvykle pro řidiče již viditelný cílový výjezd OK, proto má v místě odpojení z okružního pásu (KT2 = TK3) podobný vliv původní rychlost na vjezdu V, poloměr ROUT a úhel výjezdu β,
- je při jízdě po výjezdovém oblouku ovlivněno jeho poloměrem ROUT a úhel výjezdu β a v následujících bodech se již snaží vrátit ke své původní (vjezdové) rychlosti V.
Korelace vypovídá o vztahu mezi aktuální rychlostí V a prvky směrového polygonu. Rychlost na průjezdu OK je ovlivněna geometrií OK. Obdobných výsledkům dosáhla i studie rychlostních charakteristik na přímém průjezdu OK [03]. Největší korelace byla zaznamenána mezi rychlostí před vjezdem na OK (V50 před vjezdem) a rychlostí se všemi následujícími body průjezdu. To značí, že se chování řidiče v průběhu průjezdu OK nemění (pokud řidič vjíždí vysokou rychlostí do OK, tak průjezd a výjezd z OK provádí také vysokou rychlostí a naopak).
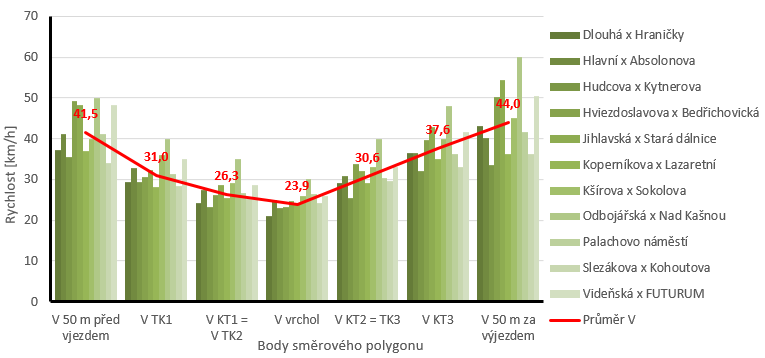
Na následujícím obr. 08 je zobrazen průběh průměrné rychlosti V měřícího vozidla (červená čára) z 92 realizovaných průjezdů. Rychlost je nejnižší ve vrcholové části oblouku, který náleží okružnímu pásu křižovatky. Zelené sloupce udávají hodnotu průměrné rychlosti V z jednotlivých trajektorií průjezdu v rámci konkrétní křižovatky. Vyšší hodnoty rychlostí odpovídají nízkým hodnotám směrového úhlu α a velkému poloměru R. Což vede k přímému průjezdu křižovatkou.
|
|
|
obr. 08.Rychlost měřícího vozidla na přímém průjezdu OK v bodech směrového polygonu |
Diskuze a závěr
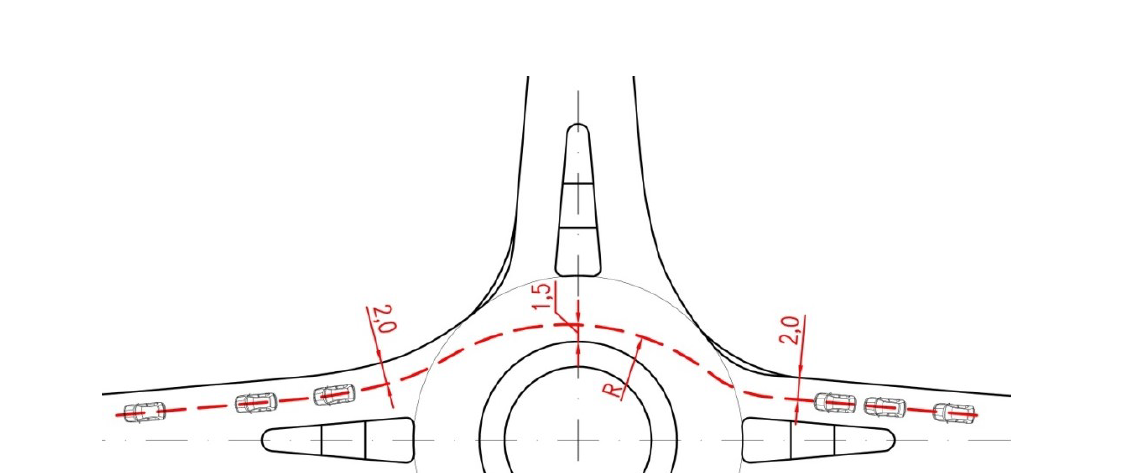
Dle revidovaného vydání TP 135 [02] je požadováno vychýlení trajektorie osobního automobilu na přímém průjezdu OK. Toto vychýlení má být zajištěno rozměry a umístěním středového ostrova a prstence spolu s ostatními prvky okružní křižovatky. Trajektorie pohybu vozidla se uvažuje dle následujícího obr. 09. Současně je zde popsán požadavek, že odchylka dráhy vozidla projíždějícího OK mezi dvěma protějšími nebo sousedními paprsky křižovatky nemá umožnit rychlost vyšší jak:
- 30 km/h na OK s jedním pruhem na okruhu,
- 50 km/h na OK se dvěma a více pruhy na okruhu.
|
|
|
obr. 09.Trajektorie průjezdu vozidla JOK (D=30 m) pro výpočet dosahované rychlosti na okružním pásu. |
V této práci jsme však identifikovali vliv poloměru vjezdu RIN dle korelace a úhlu na vjezdu α dle bezpečnostní funkce. Model nehodovosti vjezdové části trajektorie (viz vzorec (1)) identifikoval vliv: intenzity I, úhlu na vjezdu α a přibližující se rychlosti vozidla. Model předpokládá, že:
- s rostoucí hodnotou intenzity bude počet očekávaných nehod N klesat,
- s rostoucí hodnotou úhlu na vjezdu α bude očekávaný počet nehod N klesat,
- a že s rostoucí hodnotou přibližující rychlost bude očekávaný počet nehod N růst.
|
|
[-] |
Vliv rostoucí hodnoty intenzity I na vzrůstající počet nehod N lze vysvětlit vyšším podílem malých mezer. Což má za následek menší rozestupy mezi vozidly, přirozeně nižší rychlost a větší pozornost řidičů. Nízké hodnoty úhlu na vjezdu α vedou k pocitové přednosti v jízdě a vyšší rychlosti vozidel, což je nebezpečné. Hodnotu vysokých přibližujících rychlostí vozidel na vjezdu není třeba komentovat. Před závěrem je nutné podotknout, že tato práce pouze shrnuje počáteční sběr a analýzu dat. Je zanedbána rozmanitost vozového parku, řidičů a průjezdová křivka vozidla byla nahrazena kružnicí.
Z výsledků korelace a multifaktorové analýzy vyplývá, že parametry směrového polygonu trajektorie na přímém průjezdu OK jsou ovlivněny parametry vjezdu, a to následovně:
- poloměr vjezdu RIN ovlivňuje přibližovací rychlost vozidla,
- úhel na vjezdu α má vliv na vznik nehody, současně koreluje s poloměrem vjezdu RIN.
Vjezdy OK je tedy vhodné navrhovat s dostatečným směrovým vychýlením (α > 0) a poloměrem vjezdu RIN. Požadavky na směrové vychýlení na vjezdu OK nejsou však v současném znění TP 135 dostatečně specifikovány. TP řeší vjezd pouze poloměrem průjezdu, na kterém je posuzována dosahovaná rychlost směrodatného vozidla a jeho příčné zrychlení. Vyšší hodnoty směrového úhlu α zamezí řidiči vidět přímo skrz křižovatku a podpoří tak přednost v jízdě na okruhu. Toto zjištění by mělo být promítnuto do dalších úprav TP 135.
Poděkování
Tento článek byl vytvořen za finanční podpory Ministerstva školství, mládeže a tělovýchovy v rámci programu Národní program udržitelnosti I, projektu Dopravní VaV centrum (LO1610) a na výzkumné infrastruktuře pořízené z Operačního programu Výzkum a vývoj pro inovace (CZ.1.05/2.1.00/03.0064).
Literatura, reference
- ČSN 73 6102 Projektování křižovatek na silničních komunikacích, edice č. 2, červen 2012, Úřad pro technickou normalizaci, metrologii a státní zkušebnictví, 2012
- TP 135 Projektování okružních křižovatek na silničních a místních komunikacích, Ministerstvo dopravy ČR, duben 2017
- Sangyoup K., Jaisung Ch., Safety Analysis of Roundabout Designs based on Geometric and Speed Characteristics, KSCE Journal of Civil Engineering (2013) 17(6):1446-1454, DOI 10.1007/s12205-013-0177-4
- Bared J. G., Prosser W., Esse C. T., State of the Art Design of Roundabouts, Transportation Research record 1579, No. 970969
- Design Guide on Inter-Urban Roundabouts (in French). SETRA, France, 1996.
- Beau B., Alsghan I., Li-Hong Chiu, Andrea R. Bill, and David A. Noyce, Analysis of Rear-End Collisions at Roundabout Approaches, Transportation Research Record: Journal of the Transportation Research Board, No. 2585, Transportation Research Board, Washington, D.C., 2016, pp. 29–38. DOI: 10.3141/2585-04
- Turner S. A., Roozengurg A. P., Smith A. W., Roundabout crash prediction models, June 2009, NZ Transport Agency research reposrt 386.
- Roundabouts – Application and design, A practical manual, Ministry of transport, Public Works and Water management, partners for Roads, June 2009, file: B5381-01.001, registration number: VB/SE2008.0772
- Nicholas J. Garber, Lester A. Hoel, Traffic and Highway Engineering 5th Edition, ISBN-13: 978-1133605157, ISBN-10: 113360515X


Komentáře
Abyste mohli přidávat komentáře k tomuto článku, musíte být přihlášeni.
Klíčová slova: Okružní křižovatka, bezpečnost, trajektorie, úhel na vjezdu, úhel na přímém průjezdu, úhel na výjezdu, poloměr, rychlost
Popis: Stanovení vlivu geometrie okružní křižovatky na rychlost průjezdu a bezpečnost




 Zdroj: TP 135
Zdroj: TP 135